“Mathematics is, in its way, the poetry of logical ideas.” - Albert Einstein
Introduction
Mathematics is the study of the science of numbers! We use mathematics to develop our understanding of abstract number (pure mathematics) or mathematics applied to the real world, for example in physics, engineering or physical education (applied mathematics).
At SHIVALIK PUBLIC SCHOOL, JAITU we use maths lessons to develop students’ reasoning and communication skills, as well as logic and critical thinking. Through hard work and determination, students will be able to frame problems using mathematics, and in so doing, find efficient and effective solutions to those problems.
Our vision is to
Provide students with core knowledge and deep learning that challenges them with ambition and aspirations so that they can understand the world around them.
Intent Why do we teach this? Why do we teach it in the way we do?
Mathematics is an important creative discipline that helps us to understand and change the world. We want all pupils at SHIVALIK PUBLIC SCHOOL JAITU to experience the beauty, power and enjoyment of mathematics and develop a sense of curiosity about the subject with a clear understanding. We foster positive can-do attitudes, and we promote the fact that ‘We can all do maths!’ We believe all children can achieve in mathematics and teach for secure deep understanding of mathematical concepts through manageable steps. We use mistakes and misconceptions as an essential part of learning and provide challenge through rich and sophisticated problems.
We aim for all pupils to:
Implementation What do we teach? What does this look like?
Our whole curriculum is shaped by ourschool vision which aimsto enable all children, regardless of background, ability, additional needs,to flourish to become the very best version of themselves they can possibly be. We teach the National Curriculum, supported by a clear skills and knowledge progression. This ensures that skills and knowledge are built on year by year and sequenced appropriately to maximize learning for all children
Impact What will this look like?
By the time children leave our school they will: By the end , we aim for children to be fluent in the fundamentals of mathematics with a conceptual understanding and the ability to recall and apply knowledge rapidly and accurately. They should have the skills to solve problems by applying their mathematics to a variety of situations with increasing sophistication, including in unfamiliar contexts and to model real-life scenarios. Children will be able to reason mathematically by following a line of enquiry and develop and present a justification, argument or proof using mathematical language.
“Alone we can do so little; together we can do so much” - Helen Keller
Getting students to interact in the classroom is the call, and at the same time, it is a challenge for our lesson planning! Collaborative math activities in the classroom can help students developing skills for effective dialogue, an important life skill for all learners. Not only will pupils learn mutual understanding and respect for an increasingly globalised world, it also celebrates diversity of thought and experience. They can practice their social-emotional skills like:
“Don’t wait for the right opportunity: create it.” - George Bernard Shaw
The wider student experience is central to our departmental ethos. We have embedded enrichment activities throughout the curriculum as well as numeracy activities during form time for students to move fluently between representations of mathematical

ideas developing their mathematical reasoning in solving problems.
In addition, we train highly able students for entry into the . This further stimulates students’ interest in the subject, as well as providing them with a prestigious and well recognized award
“Respect for ourselves guides our morals; respect for others guides our manners” - Laurence Sterne
How we promote mutual respect in the Maths classroom
“If I cannot do great things, I can do small things in a great way” - Martin Luther King Jr.
Excellence in mathematics education requires equity — high expectations and strong support for all students. Becoming confident and competent as a problem solver is a complex process that requires a range of skills and experience. As teachers we can support this process in three principal ways:
Assessment is fundamental to the process of teaching and learning in Mathematics and forms an important part in the lives of pupils and teachers. The purpose of assessment are as follows:
Internal assessments take place at the end of each unit of work, which is every half term. Exams will be assessed at two levels; foundation tier to achieve grades 5 to 1 and higher tier for targeting grades 9 to 4. In Year 11, pupils complete three external written exam papers which forms 100% of their GCSE grade for Mathematics at the end of the year. There is one non-calculator and there are two calculator papers. Each exam paper will last 1 hour 30 minutes and will be scored out of 80 marks.
Models of Excellence
In Maths department, pupils always strive for excellence. Expectations are high for both staff and pupils. Students are encouraged to be proactive and take pride in their work.
In Mathematics students are encouraged to analyse questions and pick out key facts. This skill empowers our students to effectively solve problems in a manner that maximises their understanding and marks gained per question. Students are also encouraged to read and explain in their own words what they think a question is asking them. As a department we identify misconceptions and students are encouraged to listen through constructive verbal feedback. As a follow up, students are encouraged to make condensed notes about verbal feedback next to an error in a question, note cards or Progress Points.
Homework is work that is set to be done outside the timetabled curriculum. It contains an element of independent study in that it is not usually directly supervised by a teacher. It is important in raising student achievement.
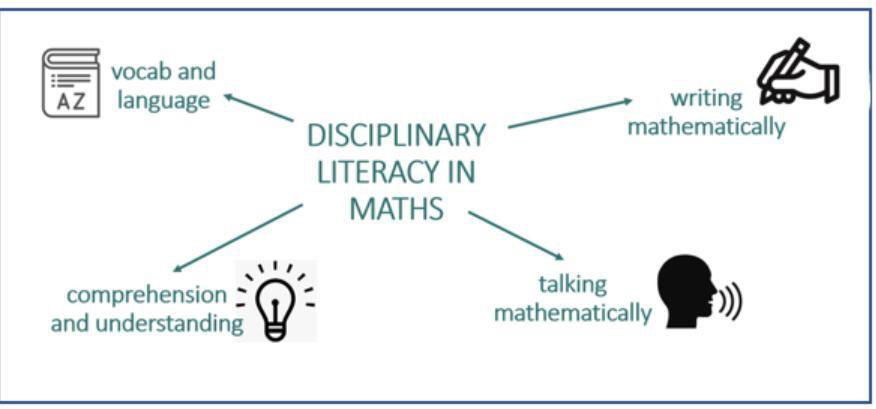
Disciplinary literacy
By teaching mathematical vocabulary as well as mathematical concepts, you are promoting conceptual understanding amongst learners. By supporting their acquisition of mathematical language, you are helping them to read and interpret problems successfully and as Cobb (1998) suggests, as children develop mathematics language, they learn to communicate and share universal mathematical concepts and operations with their peers and others.
Homework enhances pupil learning, improves achievement and develops students' study skills and as such is an integral part of the curriculum. It requires careful planning and integration into the scheme of work of each curriculum area.
So what are the key things to think about when teaching new maths terms?
1. Pre-teaching new language
Introduce learners to new language before you introduce them to new procedures. When you teach a new word at point-of-use, the word can be lost or misunderstood as learners struggle with a new concept. To take ‘probability’ as an example, start learners off by explaining that the new word is a noun and it is the name we give to the likelihood of something happening
2. Develop nuanced understanding
If you want to help learners develop a more nuanced understanding of terms and their characteristics, here are some ideas to try:
The Frayer model: When defining an abstract concept, it is useful to think about what that idea IS and IS NOT. The Frayer model encourages learners to think about the defining characteristics of a concept
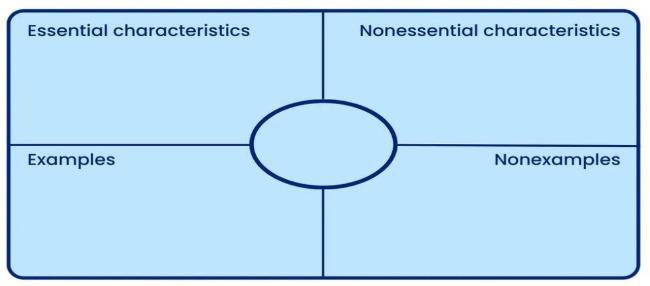
So, to take ‘Prime Numbers’ as an example, essential characteristics include the fact that a prime number has exactly two positive divisors, 1 and the number itself. Non-essential characteristics include the bservation that prime numbers are usually odd
Once you’ve introduced the new word and the new concept, try using this step-by-step guide to improving understanding.
What are Literacies within the Disciplines? The following lists for each of the major content areas, while not comprehensive, can act as starting points through which communities of teachers can begin to think in terms of disciplinary literacy (Lent, 2016)

What professional development opportunities will you provide for teachers within your team?
Regularly share good practice – lesson resources, marking and feedback examples, teaching for SEN, etc.
Open door policy – any staff can walk into Maths leadership team lessons to observe and get ideas on developing their own practice
Department time to be robust and focused on key areas of development Use of key
books to support pedagogy e.g., ‘Teaching Walkthroughs’ Use of key books to
support subject knowledge e.g., ‘Maths curriculum
Support with reading and literacy from whole school
How will you as a subject leader monitor and evaluate the impact?
Regular departmental drop-ins and learning walks with key focus area feedback will be shared each time this happens Half termly book reviews Student voice every term
Mastery
The mastery approach in Maths involves breaking down larger, complex learning goals into smaller, more manageable steps. Teaching maths for mastery offers all pupils access to the full maths curriculum. This inclusive approach, and its emphasis on promoting multiple methods of solving a problem, builds self-confidence and resilience in pupils.
We believe the ‘mastery approach’ to teaching is the underlying principle of securing a deep understanding. At Rockwood, we use Mathematics Mastery to equip every child with the mathematical thinking and problem-solving kills necessary to succeed in all areas of their lives, as children and as adults. Instead of learning mathematical proceduresby rote, we want pupils to build adeep conceptual understanding of concepts, which will enable them to apply their learning in fferent situations. To achieve this, we ensure that each lesson is based around three key principles of learning, Conceptual Understanding, Mathematical Thinking and Language and Communication. These principles underpin maths learning at Ridgeway and nable all children to communicate their understanding clearly using a wide range of mathematical vocabulary, reason,challenge and explain their learning in order to solve problems and create a well-rounded, deep understanding of mathematicalconcepts.
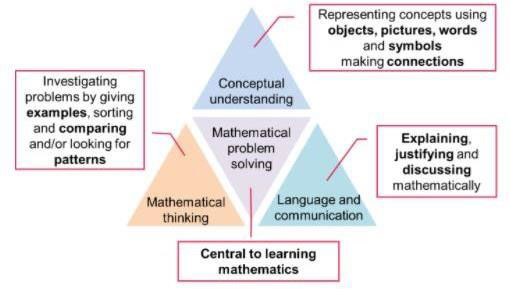
Impact of Mastery approach:
Whole class moves through content at the same pace
When teaching for mastery, the whole class moves through topics at broadly the same pace. Each topic is studied in depth and the teacher does not move to the next stage until all children demonstrate that they have a secure understanding of mathematical concepts
Time to think deeply about the maths
Students are given time to think deeply about the maths and really understand concepts at a relational level rather than as a set of rules or procedures. This slower pace leads to greater progress because it ensures that students are secure in their understanding and teachers do not need to revisit topics once they have been covered in depth.
Builds self-confidence in learnerss
In a traditional maths lesson, children are put in different groups and given different content based on their anticipated ability. This means that from an early age child are classed as those who can and cannot “do maths”. Teaching maths for mastery is different because it offers all pupils access to the full maths curriculum. This inclusive approach, and its emphasis on promoting multiple methods of solving a problem, builds self-confidence and resilience in pupils.
Differentiates throughdepthrather than acceleration
Though the whole class goes through the same content at the same pace, there is still plenty of opportunity for differentiation. Unlike the old model, where advanced learners are accelerated through new content, those pupils who grasp concepts quickly are challenged with rich and sophisticated problems within the topic. Those children who are not sufficiently fluent are provided additional support to consolidate their understanding before moving on.
Teaching Model:
It is important to have a classroom routine pupil can count on every day. Having the same procedures everyday cuts down wasted learning time significantly.
Our classroom routines promote a positive environment where all pupils can learn. Our daily routines include:
Example of what a typical science lesson would look like at Rockwood:
Pupils settle into a silent DO NOW activity at the beginning of the lesson which assess prior knowledge or involves consolidation:
Pupils transition into an “I DO/ WE DO” part to the lesson where the teacher delivers new instruction/theory or ideas. At this stage, teachers use different AFL techniques to challenge the thinking of the students
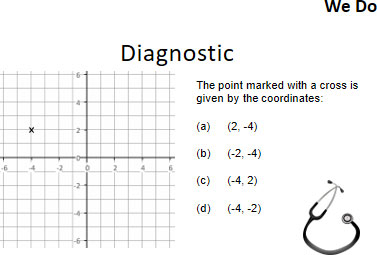
Pupils will then apply the skills they have acquired to a (YOU DO) mini plenary/ progress task and deliberate practice independently (if instructed) or with their work partner. This is usually time restricted and instant feedback is provided where pupils will then self/peer assess in red pen.
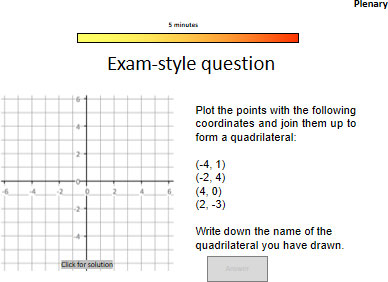
Finally, pupils will end the lesson with a plenary task which allows them to test their newly learned skills in exam style questions. This helps further strengthen and develop knowledge, understanding and application.

Mr. Khushpreet Singh (Head of Mathematics)
General oversight of all departmental policies and procedures Teaching and Learning Data and Reporting
Mrs. Neelam Bansal (2nd in department)
Lead on rewards and Whole school numeracy
Miss. Kanika Maheshwari (Coordinator)
class 1 to and 1V Lead
Mr. Madhav Goyal
Lead on Most Able and Maths social media profile and IT cell.
Ms.Shweta. Ms.Sangeeta. Ms. Geetinder kaur. Ms.Priyanka
Support with rewards, enrichment and student psychological research.